Funções

Instituto Federal do Pará
Plano Nacional de Formação de Professores da Educação Básica
Curso de Licenciatura Plena em Informática
Disciplina: Matemática para Computação
Prof.  Francisco Robson

Funções

Equipe:

Antonia Laudecir Freitas

Manoel Marivaldo dos Santos Sousa

Marta Macedo Sousa

Paulo Rogerio Melo e Silva

Santarém – Pa

Definição de Função

ƒ é aplicação de A em B ⇔(∀ x∈A, ∃!y ∈B|(x,y) ∈ ƒ)

Em uma função temos:

Domínio

Imagem

Contradomínio

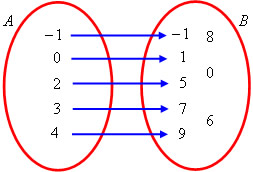
Observe os conjuntos A={-1,0,2,3,4} e B={-1,0,1,5,6,7,8,9} e a ƒ: A →B definida por y=2x+1

                                                                             

                          

                                                               

Domínio

É o conjunto formado por todos os elementos do conjunto A. Indicaremos por D(ƒ).

Assim teremos, D(ƒ)={-1,0,2,3,4}

Imagem da função

 É o subconjunto B formado pelos elementos que estão associados aos elementos do domínio.Indicaremos por Im(ƒ). Então :

Im(ƒ)= {-1,1,5,7,9}  

Dizemos que:

-1 é a imagem de -1 pela função y=2x+1.

ƒ(-1)=-1

ƒ(0)=1

ƒ(2)=5
ƒ(3)=7
ƒ(4)=9

Formando o conjunto imagem

                     

                                

                       {-1,1,5,7,9}

Contradomínio

O conjunto B é denominado contradomínio da função. Indicaremos por CD(ƒ). Então temos:

CD(ƒ)={-1,0,1,5,6,7,8,9}

Funções Iguais

*       Duas funções f e g, tais que f está definida de A em B e g está definida de C em D, são

*       iguais se e somente se  ∀ x∈A  , tem-se:

*        A = C (domínios iguais)

*        B = D (contra-domínios iguais),

*        f(x) = g(x) (leis de correspondências iguais)

Funções Parciais e Totais

Uma função parcial nada mais é do que uma relação funcional. Se a relação funcional for também total, então a denominamos de função total. Portanto podemos dizer que toda função total é uma função parcial e toda função parcial é uma relação. Entretanto,nem toda relação é uma função parcial, assim como nem toda função parcial é uma função total.


Função Parcial

Uma função parcial é uma relação funcional, ou seja, cada elemento do domínio está relacionado a no máximo um elemento do contradomínio.

*       Um elemento pertence à função parcial (a, b) ∈ f pode ser representado por f(a)=b

*       Ex: Dados os conjuntos A={a} e B={x,y} temos que a seguinte relação é função parcial:

R: B → A = {(x,a),(y,a)}


 Função total

È uma função parcial que é total. Em outras palavras, é uma função parcial definida para todos os elementos do domínio.

Dentre as funções totais podemos citar e aprofundarmos o conhecimento em diversos tipos de funções como:


  Função Par

Considere a função f(x)= - x² +4

Observe:

f(1)= f(-1)=3

f(2)= f(-2)=0

Função Par: quando para quaisquer valores simétricos de x, x ∈ D(f),ocorre f(x) = f(-x),dizemos que a função é par e seu gráfico é simétrico em relação ao eixo das ordenadas

Função Ímpar

Uma função é ímpar quando seu gráfico é simétrico em relação à origem das coordenadas.

*       Tomemos, como exemplo a função f(x): x/2
Função Bijetora

*       Dada uma função f:A →B, dizemos que f é uma função bijetora se cada elemento do contradomínio B for imagem de um único elemento de A.

                                               

Observação: Dada uma função f: A → B diz-se que:

*       f é uma função sobrejetora se Im (f)=B
Funções Inversas 

  Dados A={-2,-1,0,1,2} e B={-3,-1,1,3,5}, consideremos a função f:A→B,definida por f(x)=2x+1

                           f={(-2,-3),(-1,-1),(0,1),(1,3),(2,5)}

A essa nova função de B em A chamaremos de função inversa da função inversa da função f e indicaremos por:

ƒ-¹= {(-3,-2),(-1,-1),(1,0),(3,1),(5,2)}

Função Quadrática

Sejam a,b e c,números reais e a ≠0 chama-se função polinomial do 2º grau ou função quadrática qualquer função de IR em IR,definida por uma lei na forma:

y= f(x)= ax²+bx+c

EX1: f(x)= -2x²+3x+1

Ex2: f(x)= x²-x

Ex3: f(x)=3x²

Ex4: f(x)=2x²-3

Existem outras funções:Função constante, função identidade, função linear, função afim,função modular função composta.

Relação Inversa, Propriedade das Relações, Fecho de Uma Relação e Semelhança das Propriedades das Relações com a Informática

IFPA e PARFOR
Curso: Licenciatura Plena em Informática
Competência Curricular:  Matemática para Computação
Assunto: Relação Inversa
Professor:  Robson Alves
Alunos: Genésio Macambira
Jânio Figueiredo
Maria Zenilce Silva
Neucilene Costa

Equipe 03

Relação Inversa

Propriedade das Relações

 Fecho de Uma Relação

e

Semelhança das Propriedades das Relações com a Informática

A relação entre dois conjuntos é representada pela letra R e dá-se com a associação entre os elementos ou variáveis de um conjunto A e conjunto B.

Explicitando Conjuntos

        Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir a relação R em A×B que está apresentada no gráfico.

 

Qual resposta mostra a relação R de forma explicita?

a.R={(a,1),(b,3),(c,4),(a,3)}

b.R={(1,a),(4,a),(3,b),(c,2)}

                                                                                                             c. R={(a,1),(b,3),(c,2)}

d. R={(a,1),(a,4),(b,3),(c,2)}

A relação inversa é quando invertemos as coordenadas de todos os pares ordenados de uma relação R.

        Com a mesma relação R do exercício anterior, qual das alternativas é a relação inversa R^-1?

R^-1={(a,1),(a,4),(b,3),(c,2)}

R^-1={(1,a),(4,a),(3,b),(2,c)}

R^-1={(4,a),(2,c),(3,b)}

R^-1={(1,a),(2,c)} 

Estabelecendo a relação R entre a Matemática e a Informática

 

             No exemplo acima, temos o estabilizador cuja função é ligar e desligar os equipamentos conectados a ele. Na primeira ilustração, o botão está em 1, o que corresponde ao binário ligado, já na segunda ilustração, o botão está em 0, o que corresponde ao binário desligado. A relação entre as duas ilustrações dá-se de forma inversa.

Propriedades das relações

R é dita reflexiva se aRa para todo a ∈ A, isto é, se (a,a) ∈ R para todo a ∈ A. Ou seja, se todos os elementos se relacionam com si próprios.

Considere a serviço de exemplo as seguintes relações em um conjunto A = { 1, 2, 3, 4}

R₁ = {(1,1), (2,2), (3,3), (4,4)};

R₂ = A×A, a relação universal.

Dos exemplos citados, como A contém os quatro elementos, 1, 2, 3 e 4, uma relação R em A é reflexiva se contém os quatro pares (1,1), (2,2), (3,3), (4,4)

Uma relação é irreflexiva ou Anti-reflexiva se nenhum elemento se relaciona com si próprio.

Ex: R₃ = {(1,4), (2,1), (3,2), (4,3)};

           

Estabelecendo a relação R entre a Matemática e a Informática

           Na ilustração acima, temos o cabo de redes no qual as conexões em cores estabelecem otimização no envio e recebimento de bits na net. Cada cor corresponde a cor a ser conectada a entrada do equipamento, logo se trata do tipo de relação de propriedade reflexiva em que aRa, bRb, cRc, dRd, eRe, fRf, gRg e hRh.

 Uma relação R em um conjunto A é dita simétrica se (a,a) ∈ R toda vez que (a,a) ∈ R.

Ex  R₄ = {(1,2), (2,1), (1,3), (3,1), (1,4), (4,1)};

Uma relação anti-simétrica é tal que se aRb e bRa então a=b. Assimétrica é uma relação em que aRb implica que não bRa. Uma relação anti-simétrica em A={a,b,c}, é:

R = {(a,a),(b,b),(a,b),(a,c) }

Estabelecendo a relação R entre a Matemática e a Informática

          Na fotografia, a captura do evento dá-se de forma invertida, isto é simétrica, e somente com o processo da revelação a imagem é corrigida em posição normal. Igualmente em nosso cérebro, quando captamos os eventos diários. Nossos olhos captam a imagem que é refletida de forma simétrica no fundo dos olhos. O registro é enviado ao cérebro via sinapses e o mesmo corrige a posição da imagem. No processo digital, a quantidade de pixels é condensada e corrigida para determinar contrastes, nitidez e matiz. 

A transitividade de uma relação binária vale quando aRb e bRc implicam que aRc. Uma relação transitiva em A={a,b,c}, é:

R = {(a,a),(a,c),(c,b),(a,b)}

Estabelecendo a relação R entre a Matemática e a Informática

            Na ilustração, temos o mapeamento de rotas como exemplo de propriedade transitiva. As rotas estabelecem conexões entre si formando uma ponte que envia e recebe bits.

Relação de equivalência

Uma relação R sobre um conjunto A não vazio é chamada relação de equivalência sobre A se, e somente se, R é reflexiva, simétrica e transitiva.

Ex: Se A={a,b,c} então a relação R em AxA, definida abaixo, é de equivalência:

R = {(a,a),(b,b),(c,c),(a,c),(c,a) }

Estabelecendo a relação R entre a Matemática e a Informática

            Na ilustração, temos a junção de todas as ações acontecendo simultaneamente, logo há semelhança com a propriedade de equivalência, na qual os elementos do conjunto relacionam-se de forma reflexiva, simétrica e transitiva ao mesmo tempo.

Fecho de Uma Relação

Ps: A Equipe agradece a Todos os discentes do PARFOR e, em especial, ao Prof. Robson Alves pela comutação entre a Matemática e a Informática.

       "Parabéns a Todos e ao Prof. Robson Alves por nos sentenciar a descoberta facilitadora na compreensão das Relações, Tipos e Fechos entre as Competências em voga!!!"

Álgebra de Conjuntos

Instituto Federal do Pará
Plano Nacional de Formação de Professores da Educação Básica
Curso de Licenciatura Plena em Informática
Disciplina: Matemática e Informática
Prof. Francisco Robson
Equipe: Danilo Guimarães, Ilcilene Silva e Milena Araújo
Álgebra de Conjuntos
Consideremos (informalmente) que uma álgebra de Conjuntos é constituída de operações definidas sobre conjuntos.
Relações e Operações entre conjuntos não são a mesma coisa. Enquanto que as relações são essencialmente formas de comparar conjuntos, as operações são formas de se criar novos conjuntos a partir de conjuntos já existentes.
Uma operação é um processo escolhido a partir do qual, dados dois elementos quaisquer se pode obter um terceiro elemento da mesma natureza.
Usualmente, operações como adição e multiplicação de números inteiros são representados pelos sinais + ou x
Ex: 3+4 = 7 (3, 4, 7: elementos de mesma natureza)
      3x4 = 12 (3, 4, 12: elementos de mesma natureza)
Genericamente indicamos (a θ b) → c, sendo a, b e c de mesma natureza e θ uma operação.
1.  Reunião
•    Indicada pelo símbolo U, e definida por A U B = { x I x ∈ A ou x ∈ B}
•    Corresponde à noção de Disjunção da Lógica Proposicional.
•    O conectivo “ou” simbolizado por V, é usado para indicar que um elemento pertence a AUB quando pertence somente ao conjunto A, ou somente ao conjunto B ou a ambos os conjuntos.
Ex: A= {a, b, c, d }, B = { c, d, e, f } → A U B = { a, b, c, d, e, f }
 
1.1 Propriedades da reunião
•    Idempotente: A U A = A
•    Elemento Neutro: A ∪ ∅ = A
•    Comutativa: A ∪B = B∪A
•    Associativa: (A ∪B)∪C = A ∪(B ∪C)
2. Interseção
•    Dados dois conjuntos quaisquer A e B, a operação de interseção ou intersecção gera o conjunto com todos os elementos que são comuns ao conjunto A e ao conjunto B;
•    Corresponde à noção de Conjunção da Lógica Proposicional. Onde o conectivo  “e”, indicado por ^, é usado para indicar que x ∈ (A ∩ B ), se, e somente se, x pertencer aos dois conjuntos ao mesmo tempo.
•    A∩ B = {x | x ∈ A e x ∈ B}
Ex: A = { 5, 6, 9, 8 } e B = { 0, 1, 2, 3, 4, 5 } → A ∩ B = { 5 }
 
2.1 Propriedades da Interseção
•    Idempotente: A ∩A = A
•    Elemento Neutro: A ∩ U = A
•    Comutativa: A ∩ B = B∩A
•    Associativa: (A ∩B) ∩ C = A ∩ (B ∩C)
3. Diferença
•    Dados dois conjuntos quaisquer A e B, a operação de diferença gera o conjunto com todos os elementos que pertencem ao conjunto A, mas não pertencem ao conjunto B.
•    Definida por A – B = {x | x ∈ A e x ∉ B}
Ex : : A= { 1, 2, 3, 4, 5 } , B = { 3, 4, 5, 6, 7} → A – B = { 1, 2}

4. Complementar
•    Se B é um subconjunto de A, pode-se escrever A – B = CB, A  que se lê Complementar de B em relação a A, ou também, sendo U = conjunto universo representamos por Ā (~A ou A’) o complementar de A em relação a U.
•    Esta operação é definida por Ā = {x ∈ A | x ∉ B}
Ex: A= {1, 2, 3, 4, 5, 6} , B = {3, 4, 5, 6} → A – B = { 1, 2}
 
5. Relações entre Lógica e Teoria dos Conjuntos